1. How to divide the large image, whose pixels exceed 1000*1000 approximately. For this part, our group use MATLAB to reads the image and get the data, then compressed the image to achieve the equal length and width. Then divide the image into small blocks which are 160*160, then for each block, we do the reconstruction, at last, we combined the image. In this process, we met some dilemma.
2. The sampling rate ([0,1]) in reconstructed image. We tried to find the relationship between the sampling rate and the reconstructed quality. The relationship can be described on 2 following for a certain image:
- If the number of masks is fixed, the higher sampling rate, the better reconstructed quality will be attained.
- If the sampling rate is fixed, the higher number of masks (which does not exceed the pixels of the original image), the the better reconstructed quality will be attained.
3. How to compare the original image and the reconstructed image. We used the function called ssim(image, new_image), it would return a value which is between 0 and 1, if the value is nearer to 1, the reconstructed quality would be better.
First Part
For the first part, dealing with large image. Our group modify the reconstruction part into one function, linear_reconstruction(new_image), which pass the image as the parameter. The flowchart of this week is on the following:Our group tried different ways to implement the reconstruction.
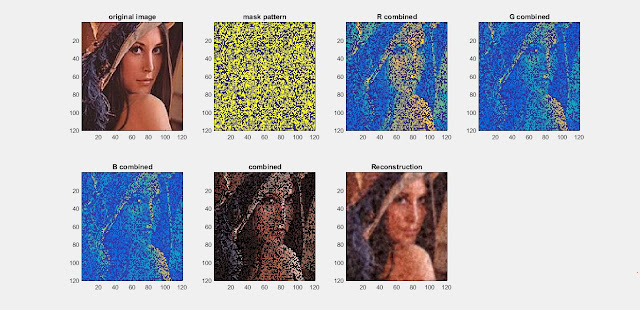
First situation result can be seen on the following:
The part in red line was cut and reconstructed. The image with title new image was the reconstructed part.
When our group tried to do the reconstruction for one specific part for the first time, MATLAB returns the area with black color.
The program takes a very long time, we did not figure out what is wrong with the program. When we tried to reconstruct the whole image, it returns the image with all black.
 |
| The Failure of the reconstruction
Our group tried the divide, reconstruction and combine the small image, and successful. Which means the algorithm of the divide has no problem.
Original Image
New Image
|
The code is under the following:
1. The reconstruction function
function [ newimg ] = linear_reconstruction( o_ima )
%UNTITLED4 Summary of this function goes here
% Detailed explanation goes here
[a,b] = size( o_ima );
if a>b
c=b;
else c=a;
end
H=im2double(o_ima);
ima=imresize(H,[c c]);
NM = 1000;
NP=c;
MaskData=zeros(NM,NP*NP);
for i=1:NM
temp=rand(NP);
temp=temp>0.5;
MaskData(i,:)= temp(:);
end
temp7=ima(:,:,1);
THzData=double(MaskData)*double(temp7(:));
newimg(:,:,1)=linear_rec(THzData, MaskData);
temp7=ima(:,:,2);
THzData=double(MaskData)*double(temp7(:));
newimg(:,:,2)=linear_rec(THzData, MaskData);
temp7=ima(:,:,3);
THzData=double(MaskData)*double(temp7(:));
newimg(:,:,3)=linear_rec(THzData, MaskData);
end
2. The main function code
[fn,pn,~]=uigetfile('*.jpg','Choose Image');
Img = imread([pn fn]);
figure(1),subplot(2,2,1),imagesc(Img), title('original image')
tic
[a,b] = size(Img);
b=b/3;
yue = 1;
for i=1:1:a
c = mod(a, i);
d = mod(b, i);
if c==0 && d==0
yue = i;
end
end
if yue>160
yue=160;
else yue;
end
b=b/3;
c=yue;
c=(c-mod(c,yue));
H=im2double(Img);
Im=imresize(H,[c c]);
%imshow(Im)
hold on
L = size(Im);
height=yue;
width=yue;
max_row = floor(L(1) /height);
max_col = floor(L(2) /width);
seg = cell(max_row,max_col);
%??
for row = 1:max_row
for col = 1:max_col
seg(row,col)= {Img((row-1)*height+1:row*height,(col-1)*width+1:col*width,:)};
end
end
for i=1:max_row*max_col
seg{i} = linear_reconstruction(seg{i});
end
for row = 1:max_row
for col = 1:max_col
new_image((row-1)*height+1:row*height,(col-1)*width+1:col*width,:) = seg{row,col} ;
end
end
for i=1:max_row*max_col
imwrite(seg{i},strcat('m',int2str(i),'.bmp')); %??i??????'mi.bmp'??
end
for row = 1:max_row
for col = 1:max_col
rectangle('Position',[yue*(col-1),yue*(row-1),yue,yue],...
'LineWidth',2,'LineStyle','-','EdgeColor','r');
end
end
hold off
figure(1),subplot(2,2,2),imshow(new_image);title('new image');
Second Part
Our group changed the sampling rate in the reconstruction process.Here are examples of fixed number of masks, different sampling rate with the similarity between the original image and reconstructed image:
160*160 pixels with 0.2 sampling rate
The similarity is 0.7850.
160*160 pixels with 0.4 sampling rate
The similarity is 0.8594.
160*160 pixels with 0.6 sampling rate
The similarity is 0.9099.
160*160 pixels with 0.8 sampling rate
The similarity is 0.9583.
160*160 pixels with 1.0 sampling rate
The similarity is approximately 1.
Under this situation, if number of masks is fixed, the higher sampling rate, the better reconstructed quality.
Under this situation, if sampling rate is fixed, the higher number of masks, the better reconstructed quality.
Third Part
Our group used the function ssim(original_image, new_image) to compare the similarity. The principle of this image is on the following [1]:ssim Structural Similarity Index for measuring image quality
- SSIMVAL = ssim(A, REF) calculates the Structural Similarity Index
(ssim) value for image A, with the image REF as the reference. A and
REF can be 2D grayscale or 3D volume images, and must be of the same
size and class.
- [SSIMVAL, SSIMMAP] = ssim(A, REF) also returns the local ssim value for
each pixel in SSIMMAP. SSIMMAP has the same size as A.
- [SSIMVAL, SSIMMAP] = ssim(A, REF, NAME1, VAL1,...) calculates the ssim
value using name-value pairs to control aspects of the computation.
Parameter names can be abbreviated.
References:
[1] Z. Wang, A. C. Bovik, H. R. Sheikh, and E. P. Simoncelli, "Image Quality Assessment: From Error Visibility to Structural Similarity," IEEE Transactions on Image Processing, Volume 13, Issue 4, pp. 600- 612, 2004.